
Informative Sites and
Phylogenetic Analyses

The input nucleotide or amino-acid sequences must be aligned. DIVEIN accepts two types of sequence files, which are fasta and phylip. The sequence data set could be in either sequential or interleaved format. The name of sequences MUST NOT contain any whitespace characters (tab or space). It is recommended that the sequence name is comprised of alphabetical characters, digits or underscore. The program will replace any other characters with underscore "_".
Example of phylip file in sequential format:
12 150 092398_316 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACAAATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT 092398_339 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACAAATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT 092398_315 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACAAATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT 092398_317 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACAAATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT 092398_312 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACAAATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT 082599_889 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACAAATTAATTGTACAAGACTCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT 082599_894 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCCAAAACCATATTAGTACAGCTGAATGAAACTGTACAAATTAATTGTACAAGACCCAACGACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT 082599_896 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACAAATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT 082599_916 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACAAATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT 082599_917 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACAAATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT ML1365_1 GAAGAAGAGGTAATAATTAGATCACAAAATTTCACAGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACAAATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT ML1365_2 GAAGAAGAGGTAATAATTAGATCACAAAATTTCACAGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACAAATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT
Example of phylip file in interleaved format:
12 150 092398_316 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA 092398_339 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA 092398_315 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA 092398_317 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA 092398_312 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA 082599_889 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA 082599_894 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCCAAAACCATATTAGTACAGCTGAATGAAACTGTACA 082599_896 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA 082599_916 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA 082599_917 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA ML1365_1 GAAGAAGAGGTAATAATTAGATCACAAAATTTCACAGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA ML1365_2 GAAGAAGAGGTAATAATTAGATCACAAAATTTCACAGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT AATTAATTGTACAAGACTCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT AATTAATTGTACAAGACCCAACGACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT
Example of fasta file:
>092398_316 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT >092398_339 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT >092398_315 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT >092398_317 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT >092398_312 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT >082599_889 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACTCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT >082599_894 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCCAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACCCAACGACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT >082599_896 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT >082599_916 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT >082599_917 GAAGAAGAGGTAATAATTAGATCACAGAATTTCACGGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT >ML1365_1 GAAGAAGAGGTAATAATTAGATCACAAAATTTCACAGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT >ML1365_2 GAAGAAGAGGTAATAATTAGATCACAAAATTTCACAGACAATGCTAAAACCATATTAGTACAGCTGAATGAAACTGTACA AATTAATTGTACAAGACCCAACAACAATACAAGAAAAAGCATACATATAGCACCAGGGAGAGCATTTTAT
DNA or amino-acid. You must select correct data type for your sequence alignment file.
2. Informative Sites
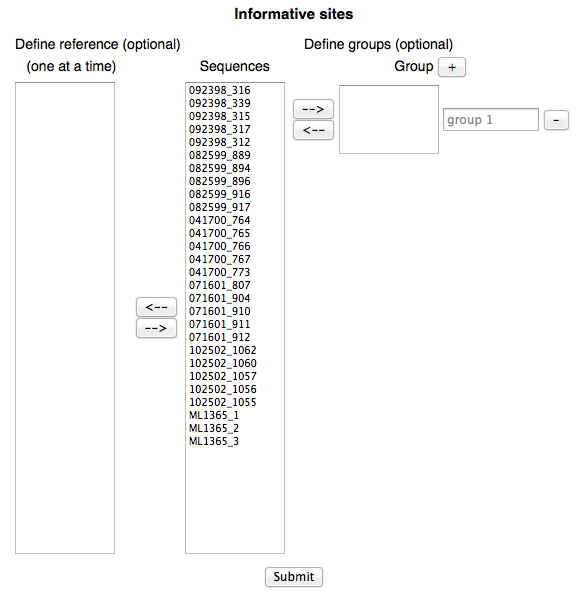
From the interface above user has options to define a reference sequence and/or group(s) of sequences of his wish. If a reference sequence is defined, DIVEIN will use it to detect informative and private sites in the alignment. If there is no reference sequence defined, DIVEIN will calculate the consensus sequence and use it as a reference to detect informative sites. If sequence group(s) are defined, DIVEIN will calculate informative sites based on each group.
2.2 Outputs
Aligned informative sites: An output file where all detected informative sites are aligned.
Example of aligned informative sites:
1334579
85120394
Consensus CGGGGGAA
Dec03_1 ....T..C
Dec03_2 ....TAC.
Dec03_3 ........
Dec03_4 GA......
Dec03_5 GA......
Mar04_1 ....T..C
Mar04_2 G.TT....
Mar04_7 .....AC.
Mar04_8 ........
Mar04_9 ..TT....
Tab-delimited informative sites & summary: A tab-delimited output file containing all detected informative sites and summary of informative sites.
Example of tab-delimited informative sites & summary:
Total_informative Informative(noGaps) 8 15 31 32 40 53 79 94
Consensus 0 0 C G G G G G A A
Dec03_1 2 2 . . . . T . . C
Dec03_2 3 3 . . . . T A C .
Dec03_3 0 0 . . . . . . . .
Dec03_4 2 2 G A . . . . . .
Dec03_5 2 2 G A . . . . . .
Mar04_1 2 2 . . . . T . . C
Mar04_2 3 3 G . T T . . . .
Mar04_7 2 2 . . . . . A C .
Mar04_8 0 0 . . . . . . . .
Mar04_9 2 2 . . T T . . . .
Alignment 8 8
A 0 2 0 0 0 2 8 8
C 7 0 0 0 0 0 2 2
G 3 8 8 8 7 8 0 0
T 0 0 2 2 3 0 0 0
Total 10 10 10 10 10 10 10 10
Aligned private sites: An output file where all detected private sites are aligned.
Example of aligned private sites:
359
5008
Consensus GGAA
Dec03_1 ....
Dec03_2 ....
Dec03_3 ....
Dec03_4 ....
Dec03_5 ....
Mar04_1 ....
Mar04_2 .C..
Mar04_7 ...G
Mar04_8 A.G.
Mar04_9 .T..
Tab-delimited private sites & summary: A tab-delimited output file containing all detected private sites and summary of private sites.
Example of tab-delimited private sites & summary:
Total_private Private(noGaps) 5 30 50 98
Consensus 0 0 G G A A
Dec03_1 0 0 . . . .
Dec03_2 0 0 . . . .
Dec03_3 0 0 . . . .
Dec03_4 0 0 . . . .
Dec03_5 0 0 . . . .
Mar04_1 0 0 . . . .
Mar04_2 1 1 . C . .
Mar04_7 1 1 . . . G
Mar04_8 2 2 A . G .
Mar04_9 1 1 . T . .
Alignment 4 4
A 1 0 9 9
C 0 1 0 0
G 9 8 1 1
T 0 1 0 0
Total 10 10 10 10
3. Center of Tree
3.1 Inputs
3.2 Outputs
Initial tree:
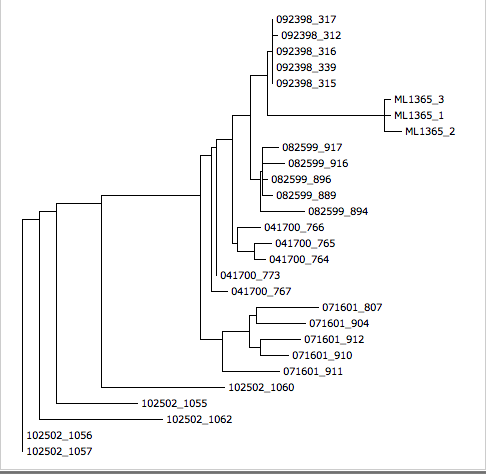 COT re-rooted tree:
COT re-rooted tree:
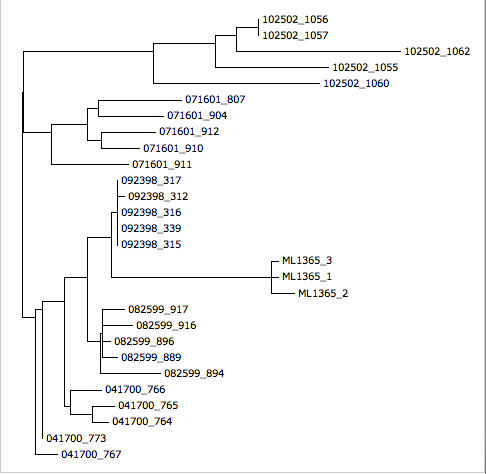
Users can perform Maximum Likelihood (ML) estimation alone or include divergence/diversity analyses through three programs (FastTree, RAxML and PhyML). They can select to calculate divergence from any or all of: MRCA, COT, consensus, or any sequence in the alignment.

From the interface above, user has options to define one or more sequences to calculate divergence from the defined sequences (MRCA, COT, consensus and any sequences in alignment), and/or to designate sequences into different groups at his wish. If user wants to calculate divergence from MRCA, he has to define outgroup sequence(s). If ingroups are defined, diversity and divergence are calculated based on each ingroup.
When an analysis is finished, a link is sent to the user by email to view and download results. Users can locally visualize and edit phylogenetic trees and dynamically generate and download graphs of distance distribution histograms and divergence and diversity (if applicable). Screen shots of DIVEIN output of phylogeney/divergence/diversity analyses are shown in the figure below.
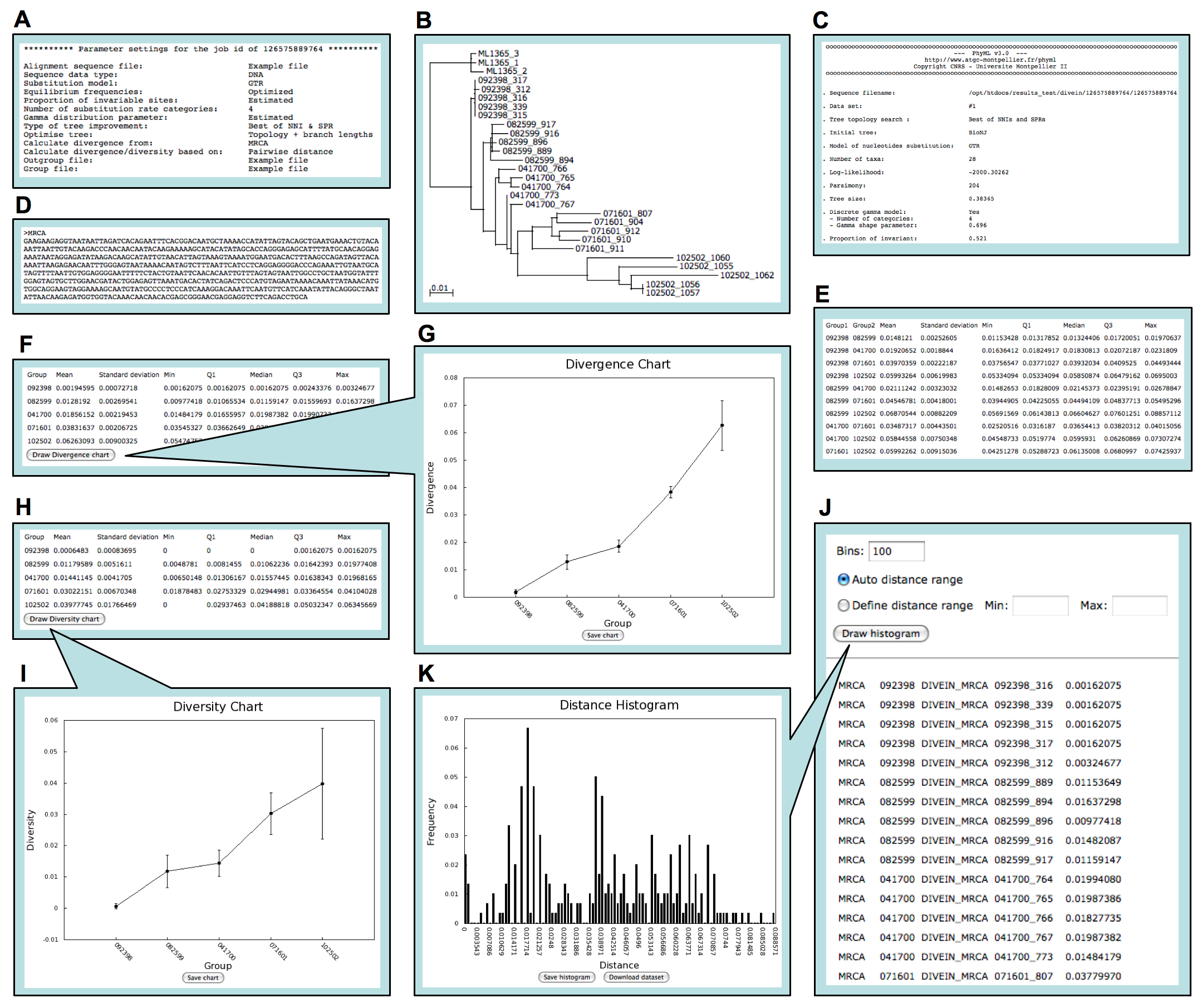
Screen shots of phylogeny/divergence/diversity output in DIVEIN. (A) Parameter settings for running the program. (B) Phylogenetic tree viewed through the Archaeopteryx Java applet. (C) Estimated evolutionary parameters. (D) Reconstructed MRCA sequence. (E) Summarized distances between groups. (F) Summarized divergence from MRCA for each group. (G) Divergence plot generated by clicking the Draw divergence chart button. (H) Summarized diversity for each group. (I) Diversity plot generated by clicking the Draw diversity chart button . (J) Distance matrix. (K) Distance distribution histogram generated by clicking the Draw histogram button.
Example:
sample1 sample1 sample1_1 sample1_2 0.01637381 sample1 sample1 sample1_1 sample1_3 0.00487810 sample1 sample1 sample1_1 sample1_4 0.00980428 sample1 sample1 sample1_1 sample1_5 0.00814550 sample1 sample1 sample1_1 sample1_6 0.01822976 sample1 sample1 sample1_1 sample1_7 0.01970637 sample1 sample1 sample1_1 sample1_8 0.01986091 sample1 sample1 sample1_1 sample1_9 0.02138145 sample1 sample1 sample1_1 sample1_10 0.01637298 sample1 sample1 sample1_2 sample1_3 0.01472954 sample1 sample1 sample1_2 sample1_4 0.01974077 sample1 sample1 sample1_2 sample1_5 0.01807237 sample1 sample1 sample1_2 sample1_6 0.02470691 sample1 sample1 sample1_2 sample1_7 0.02472565 sample1 sample1 sample1_2 sample1_8 0.02635346 sample1 sample1 sample1_2 sample1_9 0.02641488 sample1 sample1 sample1_2 sample1_10 0.02472565 sample1 sample1 sample1_3 sample1_4 0.00815682 sample1 sample1 sample1_3 sample1_5 0.00650614 sample1 sample1 sample1_3 sample1_6 0.01636412 sample1 sample1 sample1_3 sample1_7 0.01803690 sample1 sample1 sample1_3 sample1_8 0.01822346 sample1 sample1 sample1_3 sample1_9 0.01970637 sample1 sample1 sample1_3 sample1_10 0.01478813 sample1 sample1 sample1_4 sample1_5 0.01144043 sample1 sample1 sample1_4 sample1_6 0.02146014 sample1 sample1 sample1_4 sample1_7 0.02309267 sample1 sample1 sample1_4 sample1_8 0.02314722 sample1 sample1 sample1_4 sample1_9 0.02474853 sample1 sample1 sample1_4 sample1_10 0.01982461 sample1 sample1 sample1_5 sample1_6 0.01989424 sample1 sample1 sample1_5 sample1_7 0.02145289 sample1 sample1 sample1_5 sample1_8 0.02150356 sample1 sample1 sample1_5 sample1_9 0.02310453 sample1 sample1 sample1_5 sample1_10 0.01822753 sample1 sample1 sample1_6 sample1_7 0.00814550 sample1 sample1 sample1_6 sample1_8 0.01475515 sample1 sample1 sample1_6 sample1_9 0.01805260 sample1 sample1 sample1_6 sample1_10 0.01472476 sample1 sample1 sample1_7 sample1_8 0.01636654 sample1 sample1 sample1_7 sample1_9 0.01635010 sample1 sample1 sample1_7 sample1_10 0.01634613 sample1 sample1 sample1_8 sample1_9 0.01968165 sample1 sample1 sample1_8 sample1_10 0.01306167 sample1 sample1 sample1_9 sample1_10 0.00650148 sample1 sample2 sample1_1 sample2_1 0.04150894 sample1 sample2 sample1_1 sample2_2 0.04481757 sample1 sample2 sample1_1 sample2_3 0.04118581 sample1 sample2 sample1_1 sample2_4 0.04270911 sample1 sample2 sample1_1 sample2_5 0.04747813 sample1 sample2 sample1_2 sample2_1 0.05057603 sample1 sample2 sample1_2 sample2_2 0.05171311 sample1 sample2 sample1_2 sample2_3 0.04812485 sample1 sample2 sample1_2 sample2_4 0.04961091 sample1 sample2 sample1_2 sample2_5 0.05477126 sample1 sample2 sample1_3 sample2_1 0.03972601 sample1 sample2 sample1_3 sample2_2 0.04303673 sample1 sample2 sample1_3 sample2_3 0.03941800 sample1 sample2 sample1_3 sample2_4 0.04094676 sample1 sample2 sample1_3 sample2_5 0.04565166 sample1 sample2 sample1_4 sample2_1 0.04504876 sample1 sample2 sample1_4 sample2_2 0.04836577 sample1 sample2 sample1_4 sample2_3 0.04469536 sample1 sample2 sample1_4 sample2_4 0.04620262 sample1 sample2 sample1_4 sample2_5 0.05131233 sample1 sample2 sample1_5 sample2_1 0.04334661 sample1 sample2 sample1_5 sample2_2 0.04666904 sample1 sample2 sample1_5 sample2_3 0.03936277 sample1 sample2 sample1_5 sample2_4 0.04289655 sample1 sample2 sample1_5 sample2_5 0.04391926 sample1 sample2 sample1_6 sample2_1 0.03786664 sample1 sample2 sample1_6 sample2_2 0.03934172 sample1 sample2 sample1_6 sample2_3 0.02892074 sample1 sample2 sample1_6 sample2_4 0.03903859 sample1 sample2 sample1_6 sample2_5 0.03833404 sample1 sample2 sample1_7 sample2_1 0.03951028 sample1 sample2 sample1_7 sample2_2 0.03750406 sample1 sample2 sample1_7 sample2_3 0.02690821 sample1 sample2 sample1_7 sample2_4 0.03726187 sample1 sample2 sample1_7 sample2_5 0.03646500 sample1 sample2 sample1_8 sample2_1 0.03783088 sample1 sample2 sample1_8 sample2_2 0.03930404 sample1 sample2 sample1_8 sample2_3 0.03572278 sample1 sample2 sample1_8 sample2_4 0.03556032 sample1 sample2 sample1_8 sample2_5 0.04008926 sample1 sample2 sample1_9 sample2_1 0.03780811 sample1 sample2 sample1_9 sample2_2 0.03577112 sample1 sample2 sample1_9 sample2_3 0.03227438 sample1 sample2 sample1_9 sample2_4 0.02861559 sample1 sample2 sample1_9 sample2_5 0.03652437 sample1 sample2 sample1_10 sample2_1 0.03085127 sample1 sample2 sample1_10 sample2_2 0.03232153 sample1 sample2 sample1_10 sample2_3 0.02863239 sample1 sample2 sample1_10 sample2_4 0.02520516 sample1 sample2 sample1_10 sample2_5 0.03298780 sample2 sample2 sample2_1 sample2_2 0.02901092 sample2 sample2 sample2_1 sample2_3 0.02746596 sample2 sample2 sample2_1 sample2_4 0.03952009 sample2 sample2 sample2_1 sample2_5 0.02976398 sample2 sample2 sample2_2 sample2_3 0.02367655 sample2 sample2 sample2_2 sample2_4 0.04098195 sample2 sample2 sample2_2 sample2_5 0.02796319 sample2 sample2 sample2_3 sample2_4 0.03345440 sample2 sample2 sample2_3 sample2_5 0.01876146 sample2 sample2 sample2_4 sample2_5 0.03091119
Example:
sample1_1 sample1_2 0.01637381 sample1_1 sample1_3 0.00487810 sample1_1 sample1_4 0.00980428 sample1_1 sample1_5 0.00814550 sample1_1 sample1_6 0.01822976 sample1_1 sample1_7 0.01970637 sample1_1 sample1_8 0.01986091 sample1_1 sample1_9 0.02138145 sample1_1 sample1_10 0.01637298 sample1_2 sample1_3 0.01472954 sample1_2 sample1_4 0.01974077 sample1_2 sample1_5 0.01807237 sample1_2 sample1_6 0.02470691 sample1_2 sample1_7 0.02472565 sample1_2 sample1_8 0.02635346 sample1_2 sample1_9 0.02641488 sample1_2 sample1_10 0.02472565 sample1_3 sample1_4 0.00815682 sample1_3 sample1_5 0.00650614 sample1_3 sample1_6 0.01636412 sample1_3 sample1_7 0.01803690 sample1_3 sample1_8 0.01822346 sample1_3 sample1_9 0.01970637 sample1_3 sample1_10 0.01478813 sample1_4 sample1_5 0.01144043 sample1_4 sample1_6 0.02146014 sample1_4 sample1_7 0.02309267 sample1_4 sample1_8 0.02314722 sample1_4 sample1_9 0.02474853 sample1_4 sample1_10 0.01982461 sample1_5 sample1_6 0.01989424 sample1_5 sample1_7 0.02145289 sample1_5 sample1_8 0.02150356 sample1_5 sample1_9 0.02310453 sample1_5 sample1_10 0.01822753 sample1_6 sample1_7 0.00814550 sample1_6 sample1_8 0.01475515 sample1_6 sample1_9 0.01805260 sample1_6 sample1_10 0.01472476 sample1_7 sample1_8 0.01636654 sample1_7 sample1_9 0.01635010 sample1_7 sample1_10 0.01634613 sample1_8 sample1_9 0.01968165 sample1_8 sample1_10 0.01306167 sample1_9 sample1_10 0.00650148 sample1_1 sample2_1 0.04150894 sample1_1 sample2_2 0.04481757 sample1_1 sample2_3 0.04118581 sample1_1 sample2_4 0.04270911 sample1_1 sample2_5 0.04747813 sample1_2 sample2_1 0.05057603 sample1_2 sample2_2 0.05171311 sample1_2 sample2_3 0.04812485 sample1_2 sample2_4 0.04961091 sample1_2 sample2_5 0.05477126 sample1_3 sample2_1 0.03972601 sample1_3 sample2_2 0.04303673 sample1_3 sample2_3 0.03941800 sample1_3 sample2_4 0.04094676 sample1_3 sample2_5 0.04565166 sample1_4 sample2_1 0.04504876 sample1_4 sample2_2 0.04836577 sample1_4 sample2_3 0.04469536 sample1_4 sample2_4 0.04620262 sample1_4 sample2_5 0.05131233 sample1_5 sample2_1 0.04334661 sample1_5 sample2_2 0.04666904 sample1_5 sample2_3 0.03936277 sample1_5 sample2_4 0.04289655 sample1_5 sample2_5 0.04391926 sample1_6 sample2_1 0.03786664 sample1_6 sample2_2 0.03934172 sample1_6 sample2_3 0.02892074 sample1_6 sample2_4 0.03903859 sample1_6 sample2_5 0.03833404 sample1_7 sample2_1 0.03951028 sample1_7 sample2_2 0.03750406 sample1_7 sample2_3 0.02690821 sample1_7 sample2_4 0.03726187 sample1_7 sample2_5 0.03646500 sample1_8 sample2_1 0.03783088 sample1_8 sample2_2 0.03930404 sample1_8 sample2_3 0.03572278 sample1_8 sample2_4 0.03556032 sample1_8 sample2_5 0.04008926 sample1_9 sample2_1 0.03780811 sample1_9 sample2_2 0.03577112 sample1_9 sample2_3 0.03227438 sample1_9 sample2_4 0.02861559 sample1_9 sample2_5 0.03652437 sample1_10 sample2_1 0.03085127 sample1_10 sample2_2 0.03232153 sample1_10 sample2_3 0.02863239 sample1_10 sample2_4 0.02520516 sample1_10 sample2_5 0.03298780 sample2_1 sample2_2 0.02901092 sample2_1 sample2_3 0.02746596 sample2_1 sample2_4 0.03952009 sample2_1 sample2_5 0.02976398 sample2_2 sample2_3 0.02367655 sample2_2 sample2_4 0.04098195 sample2_2 sample2_5 0.02796319 sample2_3 sample2_4 0.03345440 sample2_3 sample2_5 0.01876146 sample2_4 sample2_5 0.03091119
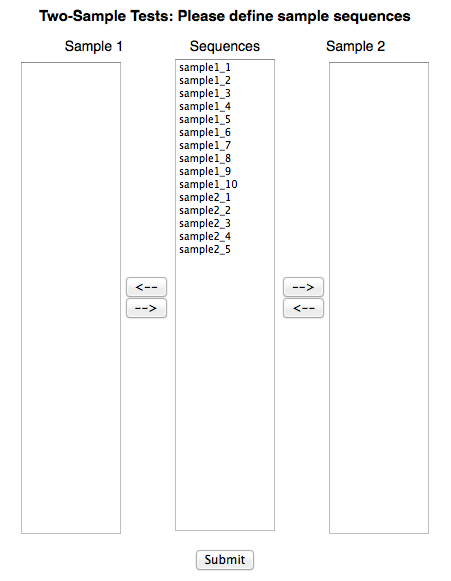
From the interface above user can designate sequences into two groups for comparison.
5.2 Outputs
P values of Z-test and T-test.
6. Sequence clustering
A genetic similarity cluster identification tool that includes two approaches to defining clusters: the first is based on pairwise genetic distance and is algorithmically similar to the approach used by HIV-TRACE (a tool developed by Sergei Kosakovksy Pond and Joel Wertheim, in wide use by the CDC); the second is based on phylogenetic branch lengths and is modified from a tool developed by Art Poon.
6.1 Inputs
6.2 Outputs
Sequence clustering CSV file
Sequence Distance matrix CSV file
Users can retrieve finished results via a previously assigned project id.
1. Lanave, C., Preparata, G., Saccone, C. & G. A. Serio. 1984. New method for calculating evolutionary substitution rates. Journal of Molecular Evolution
20:86-93.
2. Tavare, S. 1986. Some probabilistic and statistical problems on the analysis of DNA sequences. Lectures on Mathematics in the Life Sciences 17:
57-86.
3. Jukes, T. & C. Cantor. 1969. Evolution of protein molecules. In Munro, H. (ed.) Mammalian Protein Metabolism, vol. III, chap. 24, 21-132
(Academic Press, New York).
4. Kimura, M. A. 1980. Simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences.
Journal of Molecular Evolution 16:111-120.
5. Felsenstein, J. 1981. Evolutionary trees from DNA sequences: a maximum likelihood approach. Journal of Molecular Evolution 17:368-376.
6. Hasegawa, M., Kishino, H. & T. Yano. 1985. Dating of the Human-Ape splitting by a molecular clock of mitochondrial-DNA. Journal of Molecular
Evolution 22:160-174.
7. Tamura, K. & M. Nei. 1993. Estimation of the number of nucleotide substitutions in the control region of mitochondrial DNA in humans and chimpanzees.
Molecular Biology and Evolution 10:512-526.
8. Le, S. & O. Gascuel. 2008. An improved general amino-acid replacement matrix. Mol. Biol. Evol. 25:1307-1320.
9. Nickle DC, Heath L, Jensen MA, Gilbert PB, Mullins JI, Kosakovsky Pond SL. 2007. HIV-specific probabilistic models of protein evolution.
PLoS ONE 2:e503.
10. Whelan, S. & N. Goldman. 2001. A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood
approach. Molecular Biology and Evolution 18:691-699.
11. Dayhoff, M., Schwartz, R. & B. Orcutt. 1978. A model of evolutionary change in proteins. In Dayhoff, M. (ed.) Atlas of Protein Sequence and Structure,
vol. 5, 345-352 (National Biomedical Research Foundation, Washington, D. C.).
12. Jones, D., Taylor, W. & J. Thornton. 1992. The rapid generation of mutation data matrices from protein sequences. Computer Applications in the
Biosciences (CABIOS) 8:275-282.
13. Henikoff, S. & J. Henikoff. 1992. Amino acid substitution matrices from protein blocks. Proceedings of the National Academy of Sciences of the
United States of America (PNAS) 89:10915-10919.
14. Adachi, J. & M. Hasegawa. 1996. MOLPHY version 2.3. programs for molecular phylogenetics based on maximum likelihood. In Ishiguro, M. et al. (eds.)
Computer Science Monographs, 28 (The Institute of Statistical Mathematics, Tokyo).
15. Dimmic, M., Rest, J., Mindell, D. & D. Goldstein. 2002. rtREV: an amino acid substitution matrix for inference of retrovirus and reverse
transcriptase phylogeny. Journal of Molecular Evolution 55:65-73.
16. Adachi, J., P., W., Martin, W. & M. Hasegawa. 2000. Plastid genome phylogeny and a model of amino acid substitution for proteins encoded by
chloroplast DNA. Journal of Molecular Evolution 50:348-358.
17. Kosiol, C. & N. Goldman. 2004. Different versions of the Dayhoff rate matrix. Molecular Biology and Evolution 22:193-199.
18. Muller, T. & M. Vingron. 2000. Modeling amino acid replacement. Journal of Computational Biology 7:761-776.
19. Abascal F, Posada D, Zardoya R. 2007. MtArt: a new model of amino acid replacement for Arthropoda. Mol Biol Evol. 24:1-5.
20. Cao, Y. et al. 1998. Conflict among individual mitochondrial proteins in resolving the phylogeny of eutherian orders. Journal of Molecular
Evolution 47:307-322.
21. Yang, Z. 1994. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods.
J Mol Evol. 39:306-14.
22. Guindon, S. & O. Gascuel. 2003. A simple, fast and accurate algorithm to estimate large phylogenies by maximum likelihood. Systematic Biology
52:696-704.
23. Hordijk W. & O. Gascuel. 2005. Improving the efficiency of SPR moves in phylogenetic tree search methods based on maximum likelihood.
Bioinformatics 21:4338-4347.
24. Anisimova M. & O. Gascuel. 2006. Approximate Likelihood-Ratio Test for Branches: A Fast, Accurate, and Powerful Alternative. Systematic Biology,
55:539-552.
25. Stamatakis, A. et al. A rapid bootstrap algorithm for the raxml web servers, Syst. Biol., 2008, 57:758-771.
26. Stamatakis, A. Phylogenetic models of rate heterogeneity: a high performance computing perspective, Proceedings 20th IEEE International Parallel & Distributed Processing Symposium, Rhodes Island, 2006, pp. 8 pp.-.